Temperature — Intuitively and Exhaustively Explained

Making AI better by making it slightly worse

“Hotspot” by Daniel Warfield using MidJourney. All images by the author unless otherwise specified. Brought to you by the subscribers of Intuitively and Exhaustively Explained.

If you’ve played around with AI, you’ve probably encountered the term “temperature”. Temperature allows AI models to be more or less creative in their output, and thus comes up when getting AI to generate things.

In this article we’ll discuss temperature from a conceptual perspective, both in terms of AI and also the physical concept of temperature which inspired the AI approach. Once we have a solid idea of how temperature works, we’ll explore how temperature affects the output of LLMs that generate text, and even how the concept can be applied to custom models designed for custom tasks.

Before we get into the weeds, though, we’ll explore the tragically under discussed conceptual tie between AI and metallurgy.

Who is this useful for? Anyone who wants to form a complete understanding of the state of the art of AI, especially those interested in applying AI to real-world problems.

How advanced is this post? This article is great for beginners, though we will cover some slightly more advanced ideas for the more seasoned readers.

Pre-requisites: None

AI is Metal

Fun fact, I cut my teeth as a mechanical engineer and essentially stumbled on being a data scientist by accident. You might expect the two disciplines to be about as far apart from each other as STEM topics get, but actually they share a surprising and strong conceptual tie: metallurgy.

The whole idea of metallurgy is that metals, like steel, can be melted into a liquid and cooled into a solid. Liquid metals are just a bunch of atoms floating around in a soup, while solid metals generally arrange themselves in a uniform crystalline structure.

A liquid and solid metal, paired with a diagram of how the atoms which make up each are free to move through the material. Atoms are constantly moving in any material, but their temperature dictates how much they move and how freely they move.

As a metal cools into a crystalline structure, grains start to form sporadically throughout the liquid. As the metal continues to cool these grains collide with each other.

A conceptual diagram of atoms in a metal as it cools. Notice how they form into a regular crystalline grid in various locations. This is called a “grain”. Also notice how this happens at different locations throughout the metal simultaneously, resulting in boundaries between different grains. The nature of these grains, and the boundaries between them, can have significant impact on the mechanical properties of a metal.

One popular conceptualization of AI is that it’s like a metal. When you create a new AI model it’s a bunch of parameters with random values. It’s chaotic and unstructured, kind of like a liquid. As you train a model it learns certain ideas about the problem your training on, and becomes progressively more rigid, like a solid.

In metallurgy “annealing” is the concept of cooling a metal at the right speed in order to encourage certain characteristics. Similarly, in artificial intelligence, there’s a concept called a “learning rate scheduler”, Which controls how quickly the model learns throughout the training process. In fact, some of these schedulers even bare the name of “annealing”, harkening back to their metallurgical inspiration.

Cosine Annealing allows an AI model to update quickly at the beginning of the training process, then slowly reduces the rate at which it can make updates, favoring small incremental changes. In metallurgy, Annealing is the process of heating up a metal such that the grains have some movement and can settle into a different position before cooling down again.

While annealing and learning rate schedulers are cool, they’re not the topic of this article. What I want to impress, though, is that this idea of AI models being like a metal as it heats and cools has been around since the 1980s. This deep tie is part of the reason that temperature is such a fundamental idea in artificial intelligence.

Physical vs AI Temperature

Most people think of temperature as a feeling, but from a metallurgical perspective it’s more so “freedom of motion”. When something’s hot, the atoms that make up that thing vibrate around. If they get hot enough, the atoms can even jiggle around so much they fly away.

The three common states of matter, solids, liquids, and gasses, and how they relate to the movement of atoms.

Previously we discussed how very hot metals are liquids, and very cool metals are solids, but you can also have kind of hot metals that are solid, but their atoms can wiggle around more easily then a fully cooled solid. This is why blacksmiths get metal hot before they whack it with a hammer; the metal is solid, but the movement of the atoms in the metal make it malleable enough to be worked with human force.

Cold vs hot Metal. They’re similar in terms of structure, but the amount of movement of the atoms within the structure makes the metal more or less malleable.

This idea of temperature in AI is similar, except it has to do with the freedom of a models output rather than physical freedom of motion. Let’s use a language model as an example, like the ones used in ChatGPT.

The whole idea of ChatGPT, and pretty much every other language model, is that they predict which words should follow previous words. They then take whatever they predicted, feed it back into the input, and then predict a new word. This is called “autoregressive generation”

A decoder only style model, like GPT, iteratively constructing an output with autoregressive generation. From my article on ChatGPT

The way the model actually predicts a certain word is by spitting out a probability distribution. So, you give it a sequence of words, and it gives you a probability distribution of what word the model thinks should come next.

At every pass of the model, the model outputs a probability distribution. The actual word that is chosen is selected from this distribution.

A natural thing to do, then, would be to just choose the highest probability thing for every output in the autoregressive generation loop. There is a bit of a quirk with this approach, though: if you give an AI model the same input over and over, you’ll get the same output every time.

AI models are completely deterministic, meaning if you give them the same input, you’ll get the same output.

You might have noticed, if you use something like ChatGPT, you’ll get a different answer if you ask the same question multiple times.

Two different LLM responses to the same question

So, if OpenAI is using deterministic models in the backbone of ChatGPT, how is it getting different output given the same input? to promote randomness in the output, they use the fact that AI models output probability distributions.

Recall that at every pass of the model, the model outputs a probability distribution. The actual word that is chosen is selected from this distribution.

Instead of choosing the highest probability thing, when employing temperature we can choose a random thing based on how probable the different choices are. If we did that, we could get different outputs from our AI models given the same input.

If we randomly select outputs based on the probability distribution, we’ll not only get different outputs, we’ll also feed these different outputs into the input, resulting in different derivative results throughout the autoregressive generation process. This results in responses progressively deviating from one another.

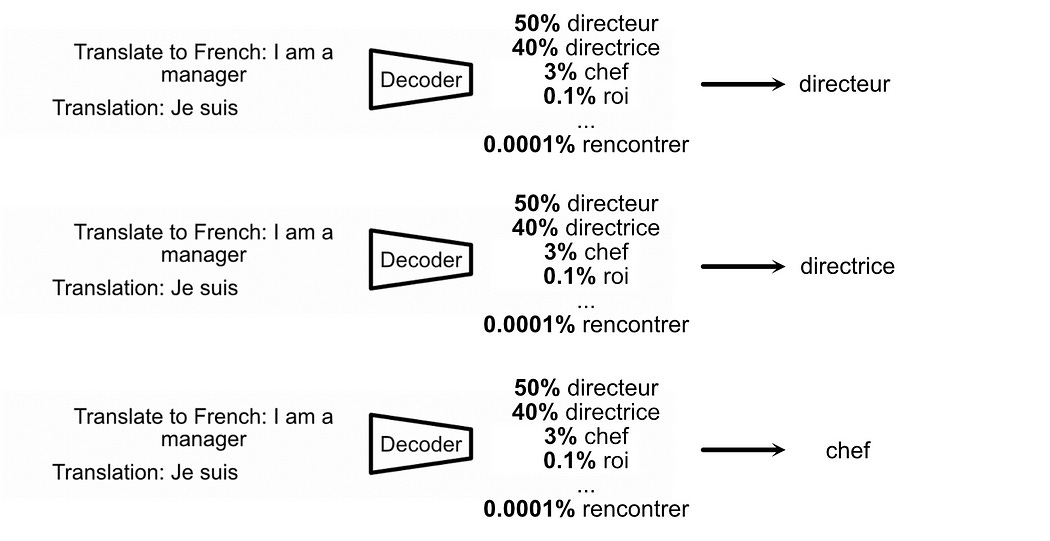
Depending on your application you might want to constrain how much randomness you allow. If you’re making an AI model write poetry you might enjoy a fairly creative spread of words, but if you’re making an AI model solve math problems you might not want it to deviate too much from the optimal choice.

Temperature allows us to dial in how much randomness we allow in the output by squashing and stretching our output distribution

temperature squashes and stretches the probability distribution before it’s used to sample a particular word, allowing data scientists to control the amount of randomness in the output.

Recall how, in metallurgy, temperature is like the “freedom of movement” of atoms. In AI, temperature is like the “freedom of movement” of a model’s output.

How Temperature Works in AI

When using temperature you set a constant, usually called t , temp, or temperature , equal to a number. temp=1 is considered to be a baseline temperature, while temp>1 encourages more random output and 0<temp<1 is less random output.

In order to manipulate the probability distribution, temperature gets applied before something called a “softmax” operation. Let’s quickly discuss that now.

---

Have any questions about this article? Join the IAEE Discord.

---

Softmax

AI models typically don’t output probabilities directly. Rather, they output numbers that might be very large or very small, referred to as logits

The output of an AI model, just a bunch of numbers

An operation called “Softmax” is applied to these numbers which turns them into a probability distribution. Big numbers become big probabilities, small numbers become small probabilities, and they all add up to 100%.

Softmax turns logits into probabilities

the math to do softmax looks like this:

The softmax function, I covered this in an article which incorporates softmax as a core component. From my article on Multi-Headed Cross Attention-By Hand

which might seem daunting if you’re not into math, so let’s break it down. First of all, in math there’s a constant e, called euler's number, but what’s important to remember is that it’s literally just a number: e=2.71828 .

we take all the raw logits output from our model and we raise e to each of those values as an exponent. We then add them up, and divide each of those exponentially raised values by the sum.

an example of applying softmax to a vector of values. Each value is raised as an exponent of e, the result is added to gether, and all exponentially raised values are divided by that sum. From my article on Multi-Headed Cross Attention-By Hand

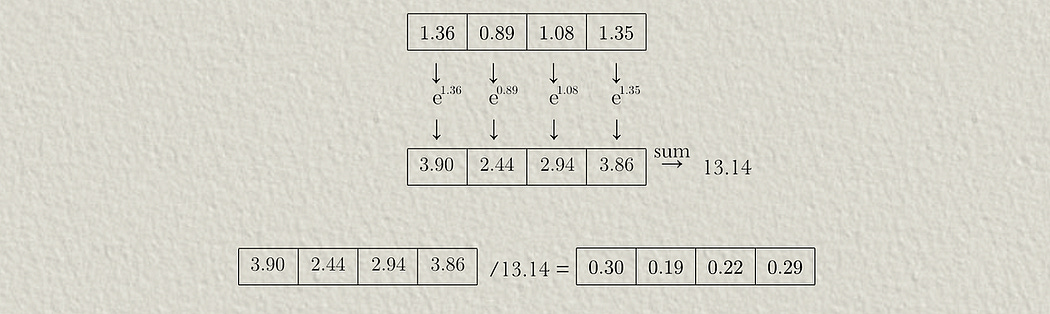
You can kind of think of this as two concepts being used at once. First you’re raising everything as an exponent of e . Because of the way exponents work, the bigger your number gets, the faster it will get bigger.

Plotting y=e^x. As you can see, as x becomes larger, the output becomes larger at an accelerated rate. This is referred to as an “exponential” relationship.

but after you’ve allowed these values to exponentially grow, you’re chopping them down to the fraction of the total value across all the examples.

After you’ve lifted all the values exponentially, you calculate the percentage of all of those values, squashing those values to a range between 0 and 1 where all values add up to equal 1. At this point they’re a probability distribution. From my article on Multi-Headed Cross Attention-By Hand

Softmax is fully represented with this mathematical expression. Here we’re saying a particular probability σ(z)i is equal to the corresponding logit raised as an exponent of e e^(zi) divided by the sum of all of the logits raised as an exponent of e Σe^(zj) .

Where Temperature Interacts with Softmax

So, this is the softmax expression without temperature:

Recall the softmax expression. Multi-Headed Cross Attention

and this is the softmax expression with temperature:

The softmax

You just divide the logits by the temperature before they’re applied as exponents to e .

For temperature values that are larger than 1, you’re scaling down the logits before they’re raised exponentially, restricting how much each probability benifits from exponential scaling. If you had a really big temperature value, say 1,000,000, all of your logits would be divided by that super big number and would be scaled down to near zero. This would make all the logits around the same size, and after softmaxing, the end result would be that each output is similarly likely. This makes unlikely outputs more likely, and likely outputs more unlikely.

For a temperature that’s smaller than 1, you’re scaling up the logits (because dividing by a number less than 1 makes that number bigger). This scales the numers up before being raised exponentially, which means big numbers are increased more than smaller numbers are. This makes outputs which were already probable even more probable.

So:

• Large Temperature → Shrinks logits → Softens the probability differences → More randomness.

• Small Temperature → Expands logits → Increases probability differences → More deterministic.

After you’ve either exaggerated the probability distribution with a low temperature, or squashed it down so that unlikely outputs are more likely with a high temperature, you then choose an output based on that probability distribution.

Using Temperature in LLMs

I have a whole bunch of articles about various LLMs, so feel free to read those if you want a more in depth understanding. For this article, we can just start with the OpenAI API.

This code asks the same LLM the same prompt four different times. Twice where the temperature is equal to zero, and twice where the temperature is equal to one.

import openai
from google.colab import userdata

# Set your OpenAI API key
API_KEY = userdata.get('OpenAIAPIKey')

# Initialize OpenAI client
client = openai.OpenAI(api_key=API_KEY)

# Define the prompt
prompt = "Write a one sentence introduction about a story of a cat detective"

# Function to query OpenAI with a given temperature
def query_openai(prompt, temperature):
    response = client.chat.completions.create(
        model="gpt-4",  # Change to "gpt-3.5-turbo" if needed
        messages=[{"role": "user", "content": prompt}],
        temperature=temperature,
        max_tokens=200
    )
    return response.choices[0].message.content

print('prompt:')
print(prompt)

# Query twice with temperature=0 (deterministic)
print('\n=====')
print('running twice with temperature=0')
print('=====')
print("First Run:\n", query_openai(prompt, 0))
print('---------------')
print("\nSecond Run:\n", query_openai(prompt, 0))

print('=====')
print('running twice with temperature=1')
print('=====')

# Query twice with temperature=1 (high variability)
print("\nFirst Run:\n", query_openai(prompt, 1))
print('---------------')
print("\nSecond Run:\n", query_openai(prompt, 1))

As expected, the output is exactly identical for the first two responses, then changes for the following two responses.

prompt:
Write a one sentence introduction about a story of a cat detective

=====
running twice with temperature=0
=====
First Run:
 In a world where animals rule, a cunning feline detective with a knack for solving mysteries embarks on a thrilling adventure to uncover the truth behind the city's most perplexing crimes.
---------------
Second Run:
 In a world where animals rule, a cunning feline detective with a knack for solving mysteries embarks on a thrilling adventure to uncover the truth behind the city's most perplexing crimes.

=====
running twice with temperature=1
=====
First Run:
 In a bustling city filled with intrigue and secrets, Whiskers, a street-savvy feline with a nose for mystery, uses his uncanny instincts and sharp wit to solve baffling crimes.
---------------
Second Run:
 In a bustling city prowled by mischief and mystery, Whiskers, an astute tuxedo cat, uses his uncanny feline instincts to unravel enigmas as the city's most unlikely, yet effective detective.

Using Temperature in a Proprietary Model

In another article, I made a transformer style model (like an LLM) that’s designed to solve Rubik’s Cubes.

Solving a Rubik's Cube with Supervised Learning — Intuitively and Exhaustively Explained

Essentially the model takes in a scrambled Rubik’s Cube, and the moves thus far, and tries to predict the next move which is most likely to result in a solved Rubik’s Cube.

The thing is, this model kind of sucks. I’m working on training it with reinforcement learning, but until then it’s been trained on a fairly small dataset and thus usually can’t solve a Rubik’s Cube that’s been scrambled by more than around 7 moves.

To get some extra juice out of this model, we can get the model to output several solutions, not just one. If we were just using the highest probability output this would be a waste of time, because we would always get the same output, but if we use temperature we’ll get many different attempts at a solution.

In this example, we can implement temperature by simply scaling the logits with temperature before applying softmax and using the resulting probability distribution to sample a move.

"""Pseudo code of applying 
"""

model_input = (scrambled_rubiks_cube, empty_move_list)

while predicting_moves:
  logits = model(model_input)
  
  # Apply temperature scaling
  if temperature != 1.0:
      y_prob = (logits / temperature).softmax(dim=-1)
  else:
      y_prob = logits.softmax(dim=-1)
  
  # Predict the next move
  predicted_next_token = torch.multinomial(y_prob, 1).squeeze(1)

  model_input = add_to_input(model_input, predicted_next_token)

thus we can use temperature to help us sample the solution space and (hopefully) stumble on a solution which the model might not have found if we only did what the model assumed was optimal.

The code used to generate this figure is farily complex, and I don’t want to distract from the nature of the article. The punchline is that I scrambled a rubik’s cube (at the top) which the model would usually struggle to solve, but I had the model generate several sequences of moves which the model thought would solve the Rubik’s cube, with a temperature of 0.2 (so, not a lot of randomness, but some randomness). That allowed the model to stumble on a few move sequences which solved the Rubik’s Cube, which you can see in cube 4, cube 5, cube 7, and cube 10.

If you’re curious about learning about this more in depth, stay tuned for my upcoming article on “Group Relative Policy Optimization”, where I use temperature to make a model learn to produce better output.

Conclusion

Is it hot in here, or did we just learn a slick new concept?

In this article we explored some interesting parallels between metallurgy and artificial intelligence, including temperature. We explored what temperature means in metallurgy, “a freedom to move”, and discussed how it occupies a similar conceptual idea in AI. We then discussed how temperature allows AI models to produce random output, how it constrains that randomness, and how the math shakes out. Finally we explored a few examples of how temperature can practically be applied to a few AI applications.