LoRA — Intuitively and Exhaustively Explained
Exploring the modern wave of machine learning: cutting edge fine tuning

Fine tuning is the process of tailoring a machine learning model to a specific application, which can be vital in achieving consistent and high quality performance. In this article we’ll discuss “Low-Rank Adaptation” (LoRA), one of the most popular fine tuning strategies. First we’ll cover the theory, then we’ll use LoRA to fine tune a language model, improving its question answering abilities.

Who is this useful for? Anyone interested in learning state of the art machine learning approaches. We’ll be focusing on language modeling in this article, but LoRA is a popular choice in many machine learning applications.
How advanced is this post? This article should be approachable to novice data scientists and enthusiasts, but contains topics which are critical in advanced applications.
Pre-requisites: While not required, a solid working understanding of large language models (LLMs) would probably be useful. Feel free to refer to my article on transformers, a common form of language model, for more information:
You’ll also probably want to have an idea of what a gradient is. I also have an article on that:
If you don’t feel confident on either of these topics you can still get a lot from this article, but they exist if you get confused.
What, and Why, is Fine Tuning?
As the state of the art of machine learning has evolved, expectations of model performance have increased; requiring more complex machine learning approaches to match the demand for heightened performance. In the earlier days of machine learning it was feasible to build a model and train it in a single pass.

This is still a popular strategy for simple problems, but for more complex problems it can be useful to think of training as two parts; “pre-training” then “fine tuning”. The general idea is to do an initial training pass on a bulk dataset and to then refine the model on a tailored dataset.
This “pre-training” then “fine tuning” strategy can allow data scientists to leverage multiple forms of data and use large pre-trained models for specific tasks. As a result, pre-training then fine tuning is a common and incredibly powerful paradigm. It comes with a few difficulties, though, which we’ll discuss in the following section.
Difficulties with Fine Tuning
The most basic form of fine tuning is to use the same exact process you used to pre-train a model to then fine tune that model on new data. You might train a model on a huge corpus of general text data, for instance, then fine tune that model using the same training strategy on a more specific dataset.
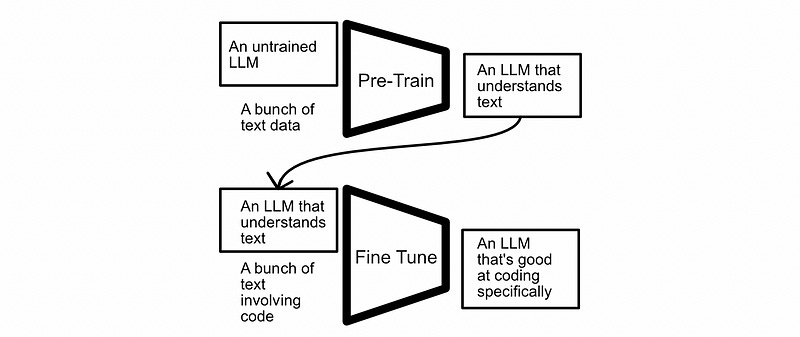
This strategy can be expensive. LLMs are absolutely massive, to fine tune using this strategy you would need enough memory to store not only the entire model, but also gradients for every parameter in the entire model (gradients being the thing that lets the model know what direction to tweak its parameters). Both the parameters and the gradients need to live on a GPU, which is why training LLMs requires so much GPU memory.
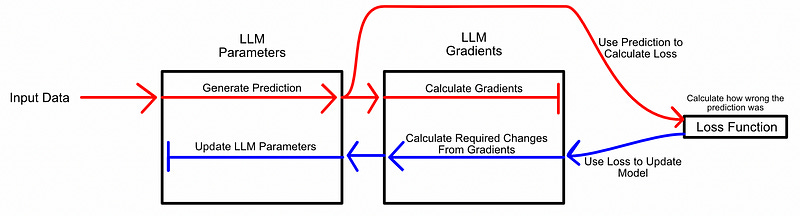
On top of the issue of storing gradients, it’s common to save “checkpoints”, which are copies of the model at a particular state throughout the training process. This is a great strategy, allowing one to experiment with the model at different phases of the fine-tuning process, but it means we need to store numerous full-size copies of the model. Falcon 180B, a popular modern LLM, requires around 360GB in storage. If we wanted to store a checkpoint of the model ten times throughout the fine-tuning process it would consume 3.6 terabytes of storage, which is a lot. Perhaps even more importantly, it takes time to save such a large amount of data. The data typically has to come off the GPU, into RAM, then onto storage; potentially adding significant delay to the fine-tuning process.
LoRA can help us deal with these issues and more. Less GPU Memory usage, smaller file sizes, faster fine-tuning times, the list goes on and on. In a practical sense one can generally consider LoRA a direct upgrade of the traditional style of fine-tuning. We’ll cover exactly how LoRA works and how it can achieve such a remarkable improvements in the following sections.
LoRA in a Nutshell
“Low-Rank Adaptation” (LoRA) is a form of “parameter efficient fine tuning” (PEFT), which allows one to fine tune a large model using a small number of learnable parameters. LoRA employs a few concepts which, when used together, massively improve fine tuning:
We can think of fine tuning as learning changes to parameters, instead of adjusting parameters themselves.
We can try to compress those changes into a smaller representation by removing duplicate information.
We can “load” our changes by simply adding them to the pre-trained parameters.
Don’t worry if that’s confusing; in the following sections we’ll go over these ideas step by step.
1) Fine Tuning as Parameter Changes
As we previously discussed, the most basic approach to fine tuning consists of iteratively updating parameters. Just like normal model training, you have the model make an inference, then update the parameters of the model based on how wrong that inference was.
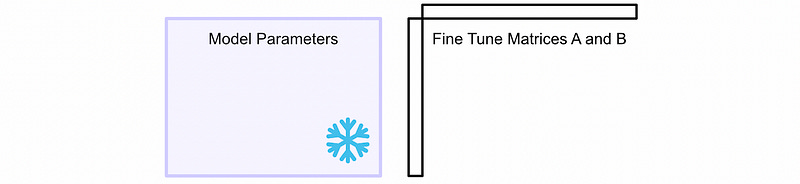
LoRA thinks of this slightly differently. Instead of thinking of fine tuning as learning better parameters, you can think of fine tuning as learning parameter changes. You can freeze the model parameters, exactly how they are, and learn the changes to those parameters necessary to make the model perform better at the fine tuned task.
This is done very similarly to training; you have the model make an inference, then update based on how wrong the inference was. However, instead of updating the model parameters, you update the change in the model parameters.
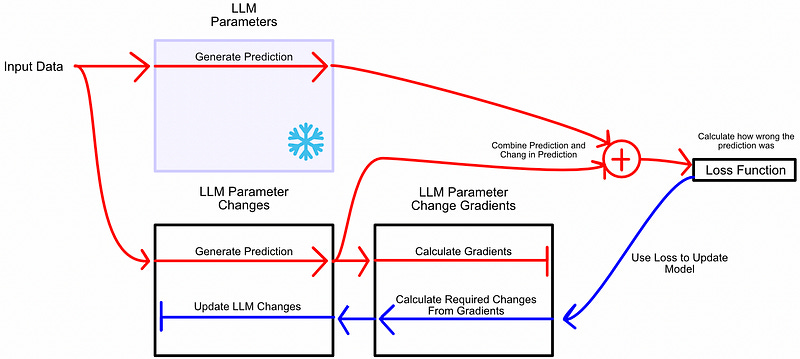
You might be thinking this is a bit of a silly abstraction. The whole point of LoRA is that we want to make fine tuning smaller and faster, how does adding more data and extra steps allow us to do that? In the next section we’ll discuss exactly that.
2) Parameter Change Compression
For the sake of illustration many represent dense networks as a series of weighted connections. Each input gets multiplied by some weight, and then added together to create outputs.
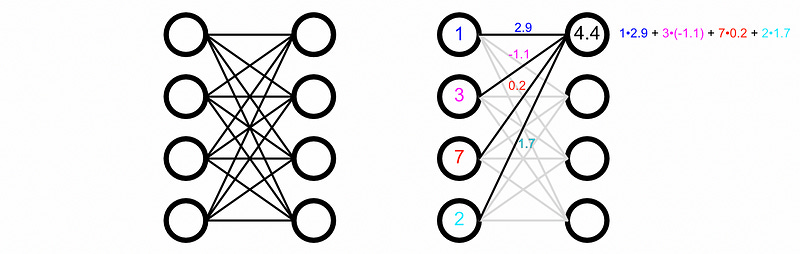
This is a completely accurate visualization from a conceptual perspective, but under the hood this actually happens via matrix multiplication. A matrix of values, called a weight matrix, gets multiplied by a vector of inputs to create the vector of outputs.

To give you an idea of how matrix multiplication works. In the example above the red dot is equal to a₁₁•b₁₂ + a₁₂•b₂₂. As you can see, this combination of multiplication and addition is very similar to that found in the neuron example. If we create the correctly shaped matrices, matrix multiplication ends up shaking out exactly identically to the concept of weighted connections.
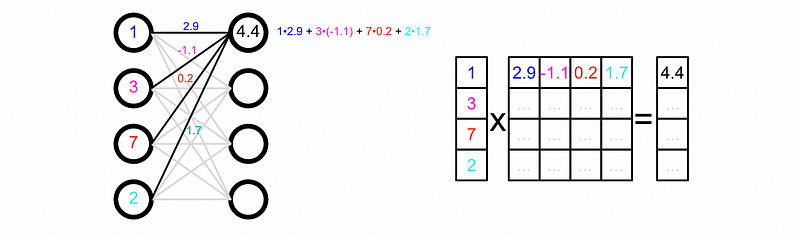
From the perspective of LoRA, understanding that weights are actually a matrix is incredibly important, as a matrix has certain properties which we can be leveraged to condense information.
Matrix Property 1) Linear Independence
You can think of a matrix, which is a two dimensional array of values, as either rows or columns of vectors. For now let’s just think of matrices as rows of vectors. Say we have a matrix consisting of two vectors which look something like this:
Each of these vectors point in different directions. You can’t squash and stretch one vector to be equal to the other vector.

Let’s add a third vector into the mix.
Vectors A and B are pointing in the same exact direction, while vector C is pointing in a different direction. As a result, no matter how you squash and stretch either A or B, they can never be used to describe C. Therefore, C is linearly independent from A and B. However, you can stretch A to equal B , and vice versa, so A and B are linearly dependent.
Let's say A and B pointed in slightly different directions.
Now A and B can be used together (With some squashing and stretching) to describe C , and likewise A and B can be described by the other vectors. In this situation we would say none of the vectors are linearly independent, because all vectors can be described with other vectors in the matrix.

Conceptually speaking, linearly independent vectors can be thought of as containing different information, while linearly dependent vectors contain some duplicate information between them.
Matrix Property 2) Rank
The idea of rank is to quantify the amount of linear independence within a matrix. I’ll skip the nitty gritty details and get straight to the point: We can break a matrix down into some number of linearly independent vectors; This form of the matrix is called “reduced row echelon form”.

By breaking the matrix down into this form (I won’t describe how because this is only useful to us conceptually), you can count how many linearly independent vectors can be used to describe the original matrix. The number of linearly independent vectors is the “rank” of the matrix. The rank of the RREF matrix above would be four, as there are four linearly independent vectors.
A little note I’ll drop in here: regardless of if you consider a matrix in terms of rows of vectors or columns of vectors, the rank is always the same. This is a mathy little detail which isn’t super important, but does have conceptual implications for the next section.
Matrix Property 3) Matrix Factors
So, matrices can contain some level of “duplicate information” in the form of linear dependence. We can exploit this idea using factorization to represent a large matrix in terms of two smaller matrices. Similarly to how a large number can be represented as the multiplication of two smaller numbers, a matrix can be thought of as the multiplication of two smaller matrices.

If you have a large matrix, with a significant degree of linear dependence (and thus a low rank), you can express that matrix as a factor of two comparatively small matrices. This idea of factorization is what allows LoRA to occupy such a small memory footprint.
The Core Idea Behind LoRA
LoRA thinks of tuning not as adjusting parameters, but as learning parameter changes. With LoRA we don’t learn the parameter changes directly, however; we learn the factors of the parameter change matrix.

This idea of learning factors of the change matrix relies on the core assumption that weight matrices within a large language model have a lot of linear dependence, as a result of having significantly more parameters than is theoretically required. Over parameterization has been shown to be beneficial in pre-training (which is why modern machine learning models are so large). The idea behind LoRA is that, once you’ve learned the general task with pre-training, you can do fine tuning with significantly less information.
learned over-parametrized models in fact reside on a low intrinsic dimension. We hypothesize that the change in weights during model adaptation also has a low “intrinsic rank”, leading to our proposed Low-Rank Adaptation (LoRA) approach. LoRA allows us to train some dense layers in a neural network indirectly by optimizing rank decomposition matrices of the dense layers’ change during adaptation instead, while keeping the pre-trained weights frozen — The LoRA Paper
This results in a significantly smaller amount of parameters being trained which means an overall faster and more storage and memory efficient fine tuning process.
Fine-Tuning Flow with LoRA
Now that we understand how the pieces of LoRA generally work, let’s put it all together.
So, first, we freeze the model parameters. We’ll be using these parameters to make inferences, but we won’t update them.
We create two matrices. These are sized in such a way that, when they’re multiplied together, they’ll be the same size as the weight matrices of the model we’re fine tuning. In a large model, with multiple weight matrices, you would create one of these pairs for each weight matrix.
We calculate the change matrix
Then we pass our input through both the frozen weights and the change matrix.
We calculate a loss based on the combination of both outputs then we update matrix A and B based on the loss

We do this operation until we’ve optimized the factors of the change matrix for our fine tuning task. The backpropagation step to update the matrices A and B is much faster than the process to update the full set of model parameters, on account of A and B being significantly smaller. This is why, despite more operations in the training process, LoRA is still typically faster than traditional fine-tuning.
When we ultimately want to make inferences with this fine tuned model, we can simply compute the change matrix, and add the changes to the weights. This means the LoRA does not change the inference time of the model.
A cool little note, we can even multiply the change matrix by a scaling factor, allowing us to control the level of impact that change matrix has on the model. In theory, we could use a bit of this LoRA and a dash of that LoRA at the same time, an approach which is common in image generation.
A Note on LoRA For Transformers
When researching this article I found a conceptual disconnect which a lot of people didn’t discuss. It’s fine to treat a machine learning model as a big box of weights, but in actuality many models have a complex structure which isn’t very box like. It wasn’t obvious to me how, exactly, this concept of a change matrix applies to the parameters in something like a transformer.

Based on my current understanding, for transformers specifically, there are two things to keep in mind:
Typically the dense network in a transformer’s multi-headed self attention layer (the one that construct the query, key, and value) is only of depth one. That is, there’s only an input layer and an output layer connected by weights.
These shallow dense networks, which comprise most of the learnable parameters in a transformer, are very very large. There might be over 100,000 input neurons being connected to 100,000 output neurons, meaning a single weight matrix, describing one of these networks, might have 10B parameters. So, even though these networks might be of depth one, they’re super duper wide, and thus the weight matrix describing them is super duper large.
From the perspective of LoRA on transformer models, these are the chief parameters being optimized; you’re learning factorized changes for each of these incredibly large, yet shallow, dense layers which exist within the model. Each of these shallow dense layers, as previously discussed, has weights which can be represented as a matrix.
A Note on LoRA Rank
LoRA has a hyperparameter, named r, which describes the depth of the A and B matrix used to construct the change matrix discussed previously. Higher r values mean larger A and B matrices, which means they can encode more linearly independent information in the change matrix.


It turns out the core assumption the LoRA paper makes, that the change to model parameters is of low implicit rank, is a pretty strong assumption. The folks at Microsoft (the publishers of LoRA) tried out a few r values and found that even A and B matrices of rank one perform surprisingly well.
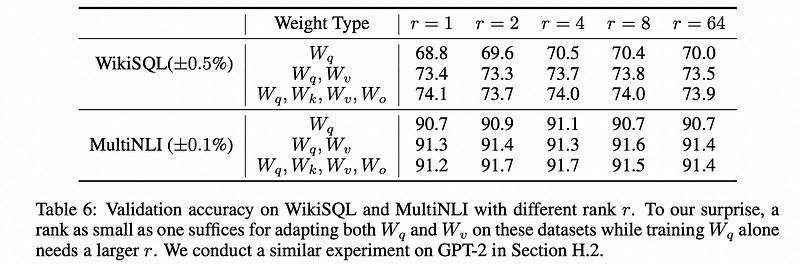
Generally, in selecting r, the advice I’ve heard is the following: When the data is similar to the data used in pre-training, a low r value is probably sufficient. When fine tuning on very new tasks, which might require substantial logical changes within the model, a high r value may be required.
LoRA in Python
Considering how much theory we went over you might be expecting a pretty long tutorial, but I have good news! HuggingFace has a module which makes LoRA super duper easy.
In this example we’ll be fine tuning a pre-trained model for question answering. Let’s go ahead and jump right in. Full code can be found here:
Keep reading with a 7-day free trial
Subscribe to Intuitively and Exhaustively Explained to keep reading this post and get 7 days of free access to the full post archives.












