KV Caching — By Hand

Doing Context Augmented Generation by hand

“Taking Note” by Daniel Warfield Using Midjourney. All images by the author unless otherwise specified. Article originally made available on Intuitively and Exhaustively Explained.

In this article, we’ll discuss “KV Caching” a method for saving generated results from previous LLM generation steps to more efficiently generate new output.

This approach is critical in efficiently serving LLM output, and also in some advanced inferencing techniques like “Context Augmented Generation” (CAG) which I discuss in this article:

Cache Augmented Generation — Intuitively and Exhaustively Explained

This article assumes you have a working understanding of “Multi-Headed Self Attention”, the primary mechanism employed in most modern LLMs. You can read more about that here:

Multi-Headed Self Attention — By Hand

It’s also assumed that you have a strong conceptual understanding of autoregressive generation, the mechanism by which LLMs generate text, and other fundamental LLM concepts. You can read more about that here:

GPT — Intuitively and Exhaustively Explained

Step 1: Defining the Input

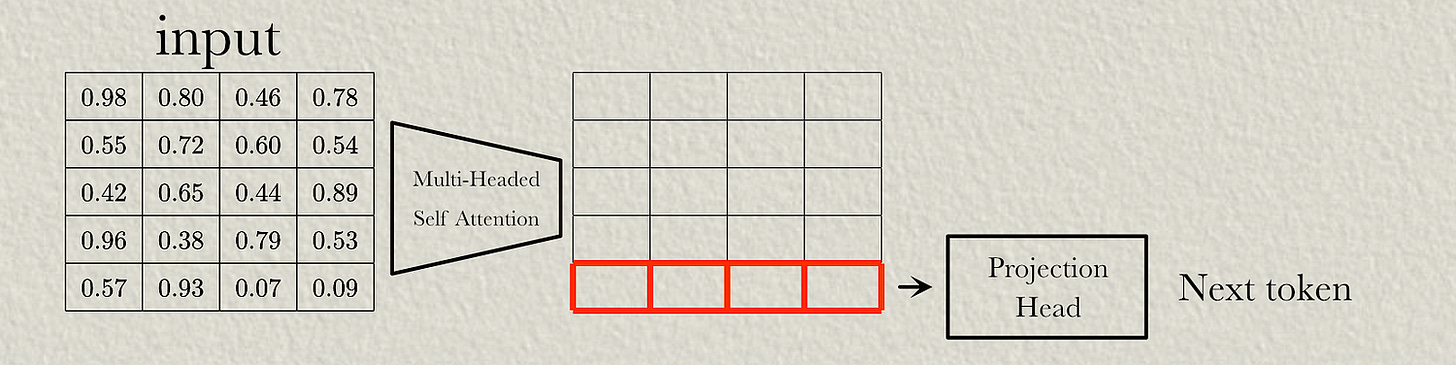
In this article, we’ll feed a sequence of text into a simplified transformer consisting of a single self-attention block.

The self attention head parameters are defined as the query weights, key weights, and value weights, as is typical in self attention.

We won’t define the projection head, but we’ll be employing it conceptually throughout this demonstration. The projection head takes outputs from the model and turns them into token predictions.

We’ll also define some input, which we’ll be passing into the model. Our model will take in this input then generate text which continues the sequence.

defining the input to the model

Step 2: Defining the Query, Key, and Value

KV Caching is only relevant during inference, and not in training the model. Thus, we’re only interested in performing a prediction based on the final token output of self attention, which corresponds to the next token being output.

To generate this output, we only need to calculate the query of the final token of the input (so, the embedded vector that corresponds to the final word).

Instead of multiplying the query weights by the entire input, if we want to calculate the next output we only need the query corresponding to that output. So, we can extract the corresponding vector from the input.

We will need the entire key and value, though.

Step 3: Calculating Attention, and Getting Output

The math is exactly the same as a naive implementation of self-attention, the only difference is that the query is a “matrix” consisting of a single vector, not a true matrix. This results in an attention “matrix” which is really just a vector of how all the input vectors should be attended together for the output token.

So, like normal self-attention, you multiply the query by the transposed key to construct the Z matrix.

Then you scale down the Z matrix by the sequence length.

This scaled Z matrix then needs to be “softmaxed” to calculate the attention matrix. This consists of raising all values as exponents of e, then dividing by the sum.

This attention “matrix” is really just a single vector that represents what percentage of each input embedding the output should consist of. This can be multiplied by the value matrix to get the output of self-attention.

We can imagine this output being passed through the projection head of the model, resulting in a token prediction. Perhaps the predicted token is the word “sequence”.

At this point, we haven’t done any KV Caching, but we have completed one output iteration which is necessary to populate the caches we will use. We can do another round of generation to explore how these caches can be employed.

Step 4: Generating a New Output with KV Caching

We might imagine the new output being embedded in a vector.

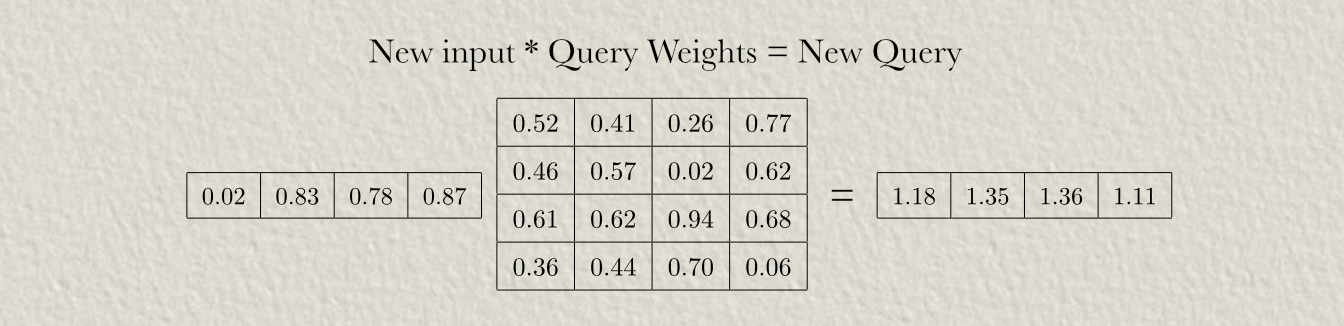
which we could feed back into the input to predict the next output token. Immediately, we can use this embedding to calculate the query.

But we’ll also need the keys and values from the entire input sequence, not just the most recent token. Fortunately, in the previous round of generation, we already computed the keys and values for all previous tokens, so instead of re-computing those we can just calculate the new key and value and append those onto the previous keys and values.

In this example, we’re only doing two rounds of autoregressive generation, but normally an LLM might do hundreds or thousands of iterations. Instead of re-computing key and value data, these caches can be saved and appended for each iteration.

We can use the key cache to calculate the attention matrix, just like how we did in the previous iteration.

And we can use the value cache, along with the computed attention, to generate the output.

This output could then be passed to the projection head, yielding a new token prediction, which could be embedded and used to calculate yet another autoregressive pass. This next pass could use the key and value caches we created in this iteration. Thus, we’re employing a cache that speeds up autoregressive generation by keeping track of the keys and values from previous iterations.